導入:2次元の回転を超えた「三次の対称性」
複素平面では、虚数単位 \( i \) が \( i^2 = -1 \) を満たすことで、 実数の一次元に対して直交する方向が生まれる。 これが「2次元」の起点であり、回転・波動・円という安定構造をもたらす。
ではもし、\( j^3 = -1 \) を満たすような数 \( j \) があったらどうなるだろうか? このとき、単なる回転だけでは表せない「三方向の対称性」が現れる。
1. 複素平面での解:正三角形の対称点
\( j^3 = -1 \) の解は次の3つ:
\[ j_1 = -1, \quad j_2 = \frac{1}{2} + i\frac{\sqrt{3}}{2}, \quad j_3 = \frac{1}{2} – i\frac{\sqrt{3}}{2}. \]
これらは複素平面上の単位円に沿って120°ずつ配置され、正三角形の頂点をつくる。 2次元ではこの3点の間を回転する円運動として理解できる。
しかし、この「三方向」は直交していない。 つまり、2次元の平面上では完全な対称性として収まらない。
2. 3次元的拡張:軸が動く回転
2次元では回転軸は固定されている。 しかし3次元では、回転軸そのものが動く自由度を得る。 このとき、\( j \) の回転はもはや平面上の円ではなく、 空間をねじる「螺旋運動」になる。
数学的には、2次元の回転群 \( U(1) \) が、 3次元の回転群 \( SO(3) \)(あるいはその被覆群 \( SU(2) \))へと拡張された状態に対応する。
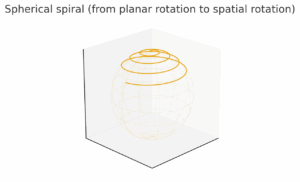
3. 螺旋の方程式:円運動の軸が傾くとき
2次元では次のように表される:
\[ z = e^{i\theta} = \cos\theta + i\sin\theta \]
3次元化するには、軸の傾きを角度 \(\phi\) として導入する:
\[ \vec{r}(\theta) = \begin{bmatrix} \cos\theta \cos\phi \\ \sin\theta \cos\phi \\ \sin\phi \end{bmatrix} \]
このとき、\(\phi\) が一定でなければ、 回転のたびに軸が傾き、球面をなぞるような螺旋軌道が生まれる。
特に、\(\phi = \frac{\pi}{3}\)(=60°)などの値をとると、 平面上の正三角形対称が空間内の正四面体対称に拡張される。
4. 四元数的な解釈:数が回転子に変わる
複素数が「平面上の回転」を表すなら、 四元数は「空間内の回転」を表す。
四元数の基本関係は:
\[ i^2 = j^2 = k^2 = ijk = -1 \]
ここでの \( j \) は、もはや単なる数ではなく「回転を生成する軸」である。 つまり、\( j^3 = -1 \) を空間的に解釈すれば、 **3次元内で120°ずつ軸を変えながら回転する動き**とみなせる。
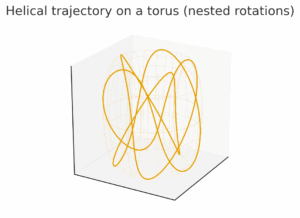
5. 軌道のイメージ:円からトーラスへ
2次元の \( j \) は円運動を描く。 3次元では、軸が傾きながら自転するため、軌道は「トーラス(ドーナツ状)」を形成する。 内側の小円が局所回転(\( i \)-型の回転)、 外側の大円が全体の回転(\( j \)-型の軸移動)に対応する。
この構造は、電子のスピンや量子波動の位相空間にも似ており、 「3乗根の回転」は実際、物理的には“場の回転対称”の抽象形として現れる。
結論:三乗根は三次元的なねじれを秘めている
\( i^2=-1 \) が2次元を開いたように、 \( j^3=-1 \) は3次元の“ねじれ”を開こうとしている。 平面では正三角形として現れるが、 それが空間に飛び出すと、螺旋・トーラス・回転対称群へと展開していく。
数は静的ではない。 その関係式が高次化するたびに、 世界はより深い次元の構造を要請する。


コメント