iとは何か:数の世界を回転させる「循環原理」
私たちが最初に「i」という記号に出会うのは、おそらく数学の授業でこう教わるときだろう。
\( i^2 = -1 \)
けれども、それがいったい何を意味しているのか── 多くの人にとって、この一文は謎のまま終わってしまう。
「なぜ、二乗してマイナスになる数があるのか?」
「そんな数は存在するのか?」
数学のなかでも、この“虚数”という概念は、長く不思議の象徴だった。
実数の限界:反転できない世界
実数の世界では、数を二乗すれば必ず正になる。 つまり、「反転する」 という現象を表すことができない。 どんなに負の数をかけても、二乗すれば正になる。 数学の世界においても、この「反対の方向」を自然に表す仕組みは存在しなかった。
しかし、もし「数に回転という概念を与えたらどうだろうか?」 そう考えたときに生まれたのが、この不思議な数 i だった。
iの本質:回転という作用
i の正体は、「数を 90° 回転させる作用」である。 それは角度の単位である θ とも似ているが、 θ が角度そのものを表すのに対して、i はその角度に 方向の力 を与える。
\( e^{i\theta} = \cos\theta + i\sin\theta \)
この式(オイラーの公式)は、i が単なる記号ではなく、 実在と潜在を循環させる原理 であることを教えてくれる。 実部(cosθ)は目に見える“現実”を、虚部(sinθ)は潜在的な“可能性”を表している。 i はその二つを回転させながら入れ替えていく。
iの意味:実在と潜在の循環
たとえば、複素数 \( a + bi \) は「実在 a」と「潜在 b」が一体となった形である。 この二つは固定された値ではなく、位相(角度)の変化によって互いに姿を変える。
\( a + bi = r(\cos\theta + i\sin\theta) \)
位相を一周( \(0 \le \theta < 2\pi\) )させると、 a と b は互いに入れ替わりながらも、全体としての大きさ \( r \) は変わらない。 つまり、実在と潜在が循環しながら保存されている。 この保存の原理こそ、i がもたらした新しい「数の法則」である。
iが生み出す世界:時間と変化
もし実数の世界が「静止した状態」を表すなら、 i はそこに「回転=時間の流れ」を与える存在である。 実数が並ぶ直線を、i は円に変える。 それは、始まりも終わりもない「循環する世界」だ。
量子力学では、この i が波動関数に登場し、 粒子の状態を変化させるための「回転の原理」として働いている。 現実の物質の運動が、目に見えない複素数の回転として描かれているのだ。
まとめ:iは存在ではなく作用
i は数ではない。 それは、「正」と「負」を往復させ、実在と潜在を結ぶ作用である。 i² = -1 とは、「180°の反転」を意味するだけでなく、 「循環による対称性の完成」をも表している。
i は、数を回すための回転軸。 数そのものではなく、変化を与える原理。 そしてその原理が、現実の中のあらゆる変化── 時間、波、力、意識──を生み出しているのかもしれない。
参考図(例)
・複素平面上の回転: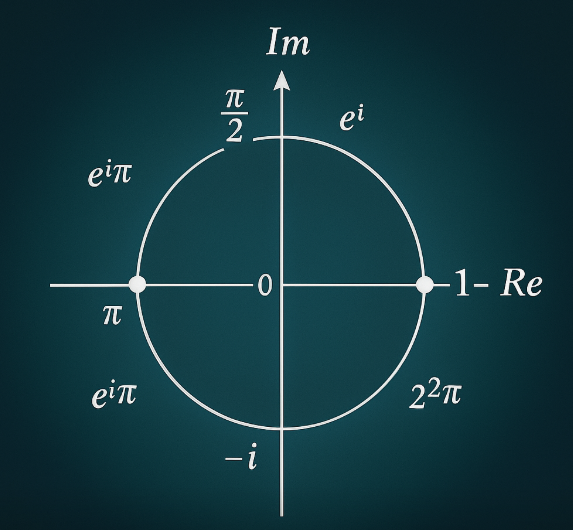
・実数世界と複素数世界の関係(z軸方向の回転):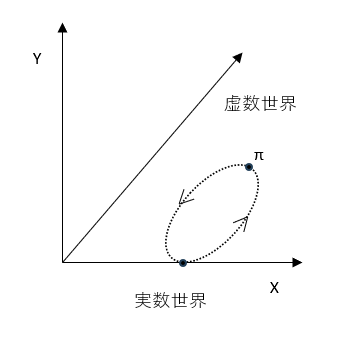


コメント