はじめに:見えない「もうひとつの数の世界」
数には、ふだん私たちが使っている「実数」のほかに、もうひとつの世界があります。
それが「虚数(きょすう)」です。
名前の通り、少し“現実離れ”して聞こえるかもしれません。
でも実は、虚数こそが私たちの世界の動き──たとえば波や回転、時間の流れ──を表すための大切な軸なんです。
複素平面:数が回転する世界
複素数とは「実数」と「虚数」を組み合わせた数です。
たとえば a + bi のように書かれ、a が現実の部分(実部)、bi が目に見えない部分(虚部)を表します。
複素数の世界では、数は線の上に並ぶのではなく、平面の上を動きます。
下の図のように、横軸が「実数の世界」、縦軸が「虚数の世界」を表しています。
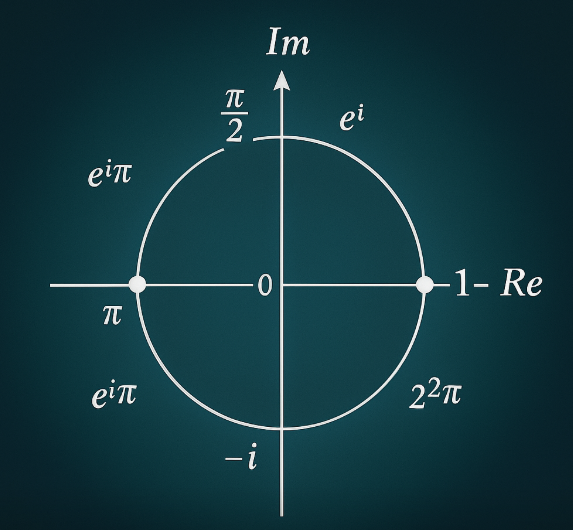
この円の動きは、次の式で表されます:
\[ e^{i\theta} = \cos\theta + i\sin\theta \]
この式は「オイラーの公式」と呼ばれます。
\(\theta\) が 0 から \(2\pi\)(1周)まで動くと、点は円をぐるっと回り、また元の位置に戻ります。
つまり虚数とは、数を回転させる力のことなのです。
実世界と虚世界:交わる瞬間だけ「現実になる」
では、そんな複素数の世界は、私たちの現実とどう関係しているのでしょうか?
そのイメージをつかむのが下の図です。
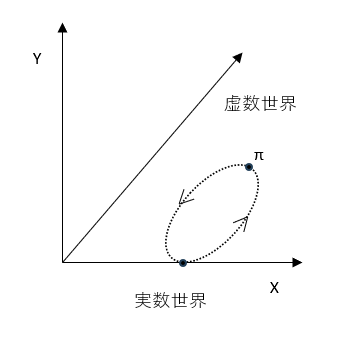
ここでは、X–Y平面が「実世界」、Z軸が「虚数の方向」を表しています。
点は、Z軸のまわりを円を描くように回っています。
そしてその円がちょうどX–Y平面(私たちの世界)と交わる瞬間、
その位置だけが「実数」として見えるのです。
たとえば角度が \(\pi\)(半回転)のときには −1、
\(2\pi\)(1周)のときには +1 に戻ります。
この回転を上から見ると「円」、横から見ると「波」に見えます。
つまり──複素数の回転が、現実の波を生んでいるのです。
複素数は、動く数
実数は「位置」を表します。
虚数は「動き」を表します。
そして複素数は、「位置と動きをひとつにした数」です。
だから、音や光、電気、そして時間の流れ──
それらの中にはすべて、複素数のような“回転のリズム”が隠れています。
数がただの記号ではなく、「世界の動きを描くもの」になったのです。
おわりに:見えない軸が、世界を回している
複素数は、実数に「回転」という次元を加えたものです。
目には見えませんが、その回転があるからこそ、
私たちの世界には波があり、時間があり、変化があります。
見えないZ軸があるから、X–Y平面は動くことができる。
虚数は、静止した世界を動かすもうひとつの軸なのです。


コメント