数学における「虚数解(imaginary solution)」とは、 実数の範囲では存在しないように見える解のことです。 たとえば、次のような方程式を考えたとき:
\[ x^2 + 1 = 0 \]
どんな実数を代入しても、この式は成り立ちません。 なぜなら、どんな数を二乗しても結果は正になるからです。 しかし数学者たちは、「それでも解を求めたい」と考えました。 そうして生まれたのが、虚数単位:
\[ i = \sqrt{-1} \]
この発想によって、「実数の外側」に新しい数の世界が広がりました。 虚数解は、実数では表せないものを“拡張的に表現する”ための道具です。 そして、その見えない構造を視覚的に理解するための方法が、ガウスの複素平面です。
1. 二次方程式と虚数解の基本
一般形の二次方程式:
\[ ax^2 + bx + c = 0 \]
解の公式は次の通りです。
\[ x = \frac{-b \pm \sqrt{b^2 – 4ac}}{2a} \]
ここで、判別式 \( D = b^2 – 4ac \) が負のとき、平方根の中がマイナスになります。 つまり、実数の範囲では解けない状況が生じるわけです。 このとき虚数単位 \(i\) を導入すると:
\[ x = \frac{-b}{2a} \pm i\frac{\sqrt{|D|}}{2a} \]
この形が「虚数解」です。 実部 \(-\frac{b}{2a}\)、虚部 \(\pm\frac{\sqrt{|D|}}{2a}\) を持つ2つの解が、 複素平面上で上下に対称に位置します。
2. ガウス平面で見る虚数解:上下に浮かぶ対称点
虚数解は、ガウスの複素平面上では次のような点になります。
\[ \left( -\frac{b}{2a}, +\frac{\sqrt{|D|}}{2a} \right) \quad \text{と} \quad \left( -\frac{b}{2a}, -\frac{\sqrt{|D|}}{2a} \right) \]
つまり、実軸の一点を中心にして、 虚軸方向に対称な2点として現れるのです。
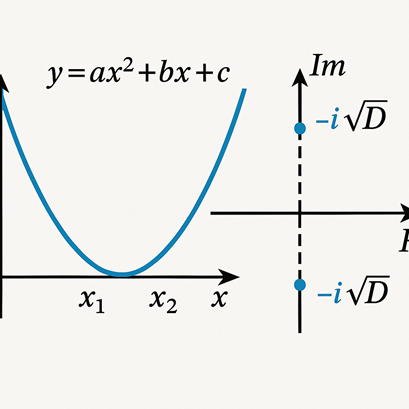
放物線が実軸と交わらない場合(判別式 D<0)、 その根は“虚軸の上下”に浮かぶ形で存在しています。 この図では、「現実の世界(実軸)」では見えないけれど、 数学的には確かに“そこにある”ということを示しています。
3. 3次元での理解:虚数解は“奥の空間”にある
次に、虚数解を3次元的に考えてみましょう。 軸を次のように設定します。
- x軸 … 実数部分(現実の横方向)
- z軸 … 虚数方向(i軸、奥行き)
- y軸 … 関数値 \(y = ax^2 + bx + c\)
この3つの軸で描くと、二次関数は“空間に浮かぶ放物面”となります。 実軸の上ではx軸と交わらない放物線でも、 奥行き方向(z軸)へ伸ばすと、その面がどこかで交わる―― それが虚数解の位置です。
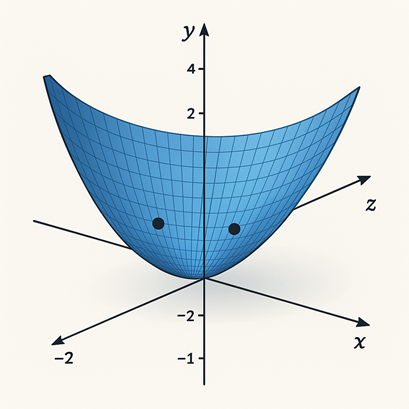
視点を変えれば、放物線が“実軸では届かない高さ”にあるが、 “少し奥の空間”に根を持っているように見えます。 これは、「現実では見えないが、理論的には確かに存在する」状態を 視覚的に表しているのです。
4. 虚数解が教えてくれること:現実を拡張する数学の思想
ガウスが複素平面を導入した理由は、 「実数では届かない問題を、より広い世界で解くため」でした。 虚数解を受け入れることは、 「見えないものを見えるようにする」数学の創造的な試みでもあります。
そしてそれは、科学や哲学にも通じる姿勢です。 直接観測できない重力、意識、情報―― それらも“見えないが確かにある構造”を仮定することで理解が進みます。
虚数は、まさにその最初の一歩でした。 “存在しないはずの数”を受け入れることで、 私たちは現実をより深く、より広く扱えるようになったのです。
5. まとめ:虚数解とは、「見えない世界を数で掴むこと」
- 虚数解は、実数では解けない方程式の「もう一つの答え」。
- 複素平面では、実軸の上下に対称な2点として存在する。
- 3次元的には、実数世界の奥行き方向に位置していると理解できる。
- それは「見えない構造を認める」ことで世界を拡張する行為である。
虚数解とは、単に数学の記号操作の結果ではなく、 「見えない世界にも秩序を見出す」人間の思考の証なのです。

コメント