導入:離散と連続のあいだにあるもの
数列がどのように変化していくかを記述する「漸化式」と、連続的な変化を扱う「微分」。これらは一見、まったく異なる世界の言語のように思えるかもしれません。しかし、両者の間には深く静かなつながりがあります。漸化式が「一歩ごとの変化」を定義するのに対し、微分は「瞬間の変化率」をとらえます。どちらも、変化という概念を形式的に表すための道具なのです。
人間が世界を理解しようとするとき、「時間」や「成長」といった現象をどのように表現するかは大きなテーマです。古代の数学者たちは、離散的な繰り返しによって数のパターンを見出し、やがて微分という連続の極限へと歩みを進めました。離散(discrete)と連続(continuous)は、数学だけでなく、思考のあり方をも二分する大きな構造です。
漸化式は、未来の値を過去の値から「計算的に」導き出します。対して微分は、変化の滑らかさを「解析的に」描き出します。この違いは、計算と解析、アルゴリズムと方程式、あるいはデジタルとアナログという対比にも通じます。現代において、この二つの視点は再び出会いつつあります。たとえば機械学習の最適化や数値解析の世界では、離散的な反復計算を通じて連続的な関数の性質を近似するのが日常です。
この記事では、「漸化式と微分」という一見異なる二つのテーマを往復しながら、変化を記述する数学的思考の本質を探ります。離散から連続へ、そして再び離散へ——その往還にこそ、私たちの世界を数理的に理解する鍵があるのです。
基礎解説:漸化式と微分、それぞれの意味
漸化式とは何か
漸化式(ぜんかしき)とは、ある数列の項を「その前の項」や「いくつかの前の項」を使って定義する式のことです。最初の値(初項)と、その後の変化のルールを与えることで、数列全体が決まります。たとえば、単純な例として次のような関係があります。
\( a_{n+1} = r a_n \)
これは「前の項に一定の比率 \( r \) を掛ける」ことで次の項を得るという漸化式です。このとき、数列は等比数列となり、一般項は \( a_n = a_0 r^n \) となります。漸化式の本質は、「繰り返しによる生成」にあります。未来を直接予測するのではなく、いまある状態から一歩ずつ未来を積み上げるのです。
この「離散的な変化のルール」は、コンピュータが得意とする思考方法でもあります。プログラムのループ構造や再帰関数は、漸化式の思想そのものです。つまり漸化式は、数列だけでなく、現代のアルゴリズムの基礎にもなっているのです。
微分とは何か
一方の微分は、連続的な変化の「瞬間的な傾き」を求める操作です。関数 \( y = f(x) \) の微分係数は、\( x \) がほんのわずかに変化したときの \( y \) の変化量を表します。式で書けば、
\( f'(x) = \lim_{h \to 0} \frac{f(x + h) – f(x)}{h} \)
となり、これは「平均変化率の極限」として定義されます。連続的な現象を数値的にとらえるために、人間が発明した最も洗練された概念のひとつです。
微分は物理学で速度や加速度を求めるだけでなく、経済学や統計学、機械学習などでも中心的な役割を担います。変化の方向や速さを知ることは、すなわちシステムを理解し、制御することに等しいのです。
漸化式と微分の共通点
漸化式と微分の根底には、「変化を記述する」という共通の意識があります。漸化式が「有限の差分」に基づくのに対し、微分は「無限に小さな差分の極限」です。つまり、微分は漸化式の連続版と考えることもできます。
たとえば、漸化式
\( a_{n+1} – a_n = k a_n \)
を、変数 \( n \) を連続量に拡張すると、微分方程式
\( \frac{da}{dn} = k a \)
が得られます。ここには、離散から連続への滑らかな橋渡しが存在します。漸化式は一歩ずつの変化を追い、微分はその流れ全体を解析的に描くのです。
この視点に立つと、漸化式と微分は対立するものではなく、むしろ同じ現象を異なるスケールで見る二つの窓のように感じられます。次章では、この関係がどのように発展してきたのか、数学史の流れの中で見ていきましょう。
歴史・文脈・発展:離散から連続へ、そして再び離散へ
漸化式の起源:繰り返しの中の秩序
漸化式の考え方は、古代からすでに存在していました。たとえばフィボナッチ数列は、次のような単純な漸化式で表されます。
\( a_{n+2} = a_{n+1} + a_n \)
この数列は「うさぎの繁殖問題」として知られていますが、その背後には「過去が未来をつくる」という漸進的な時間観があります。つまり、漸化式は単なる数学的な道具ではなく、「成長」や「進化」といった自然現象を模倣する言語でもあったのです。
中世から近代にかけて、漸化式は解析学の発展とともに形式化されていきます。特に17〜18世紀には、差分法(finite difference method)として、連続的な微分方程式を数値的に近似する技法が発展しました。これにより、漸化式は単なる数列の規則から「微分方程式を離散的に表す方法」へと進化していきます。
微分の登場:連続の極限を見つめる
一方で、微分の概念はニュートンとライプニッツによって17世紀後半に独立に確立されました。彼らは「瞬間の変化率」をとらえるための極限の思想を導入し、運動や自然現象を数学で記述する新しい時代を切り開きました。
当時の微積分学は、連続性を前提とした世界観の上に立っていました。線が途切れずに伸び、関数が滑らかに変化する——そのような「理想化された連続」の中で、微分はもっとも精密な変化の記述法となりました。
しかし現実の世界は常に連続的とは限りません。自然界には跳躍や離散的な構造があり、コンピュータの中ではデータが有限の桁数で扱われます。こうして、20世紀後半に入ると「離散化された微分」、すなわち数値微分や差分方程式が重要な役割を担うようになります。
再び出会う二つの世界
現代の数学と科学では、漸化式と微分は再び融合しつつあります。コンピュータによる数値解析は、微分方程式を離散化して解くプロセスそのものであり、アルゴリズムの反復計算は漸化式の応用です。深層学習(ディープラーニング)における「誤差逆伝播法」も、連続的な勾配(微分)を離散的に更新していく仕組みといえます。
さらに、近年では「離散微分幾何」や「差分方程式によるモデリング」など、離散と連続の中間領域を体系的に扱う分野が発展しています。そこでは、漸化式のようにステップごとに進む世界と、微分方程式のように滑らかに変化する世界の境界が、もはや明確には分かたれていません。
この流れは、私たちの時代の特徴とも重なります。デジタル化された世界において、連続的な現象を離散的に処理するという構造は、あらゆる分野に共通しています。漸化式と微分の往復は、まさに「自然と計算の対話」を象徴しているのです。
次章では、この二つの概念がどのように実際の応用や問題解決に活かされているのかを見ていきましょう。数学的な美しさが、現実の動きの中でどのように息づいているのか——そこに注目していきます。
応用・実例・ケーススタディ:変化を支配する数の言語
経済や生態における「成長の漸化式」
漸化式は、単に数学の中だけでなく、現実の世界をシミュレートする強力な道具として用いられています。たとえば、経済学における利子の計算や、人口の増加を表すモデルは典型的な応用例です。
単純な人口成長モデルとして、次の漸化式を考えます。
\( P_{n+1} = r P_n (1 – P_n) \)
これは「ロジスティック写像」と呼ばれ、人口が一定の限界に近づくと増加が抑えられるという現象を示します。この式はわずか一行でありながら、単純な値の変化からカオス(予測不能な振る舞い)を生じることがあり、数学の奥深さを象徴しています。現代の複雑系科学や非線形解析の原点にもなった方程式です。
このように、漸化式は「次に何が起こるか」を決めるシステムの最小単位といえます。デジタルな時間を一歩ずつ進めるように、シミュレーションの世界ではすべてが漸化式的に動いています。
物理や工学における「微分の世界」
一方で、微分は現象の連続的な変化を記述するために不可欠です。速度、加速度、電流、熱伝導、波動、すべてが微分方程式によって表されます。たとえば、ニュートンの運動方程式
\( F = m \frac{d^2x}{dt^2} \)
は、物体の運動を支配する最も有名な微分方程式です。力 \( F \) が与えられれば、位置 \( x(t) \) の時間変化を求めることができる。つまり、微分方程式は「自然界の法則そのもの」を表現しているといえます。
しかし、実際にこのような連続的な式を解くためには、コンピュータ上で「離散化」して計算する必要があります。たとえば時間を小さな間隔 \( \Delta t \) に区切り、次のような近似を用います。
\( \frac{dx}{dt} \approx \frac{x_{n+1} – x_n}{\Delta t} \)
これはまさに漸化式の形です。すなわち、微分方程式を解くとは、漸化式を繰り返し適用して連続的な現象を近似することにほかなりません。ここに「漸化式=離散化された微分」という対応が生まれます。
AI・最適化における「反復と勾配」
現代において、漸化式と微分の融合が最も象徴的に現れているのが、人工知能や機械学習の分野です。ニューラルネットワークの学習では、損失関数の勾配(微分)を計算し、それをもとにパラメータを更新するという反復的な手順を踏みます。この更新式は、次のような漸化式の形をしています。
\( \theta_{n+1} = \theta_n – \eta \frac{\partial L}{\partial \theta_n} \)
ここで \( \theta \) はパラメータ、\( L \) は損失関数、\( \eta \) は学習率です。これは「勾配降下法(gradient descent)」と呼ばれるアルゴリズムで、まさに「微分」と「漸化式」の融合です。連続的な勾配情報をもとに、離散的な更新を繰り返すことで最適解に近づいていくのです。
この仕組みは、まるでアナログな自然現象(微分方程式)を、デジタルな時間の中で模倣しているようにも見えます。AIの学習過程そのものが、連続と離散の調和の上に成り立っているといえるでしょう。
音・画像・データに広がる数理
さらに、デジタル信号処理(DSP)においても漸化式と微分は密接に関係しています。アナログ信号を離散化して扱う際、連続系の微分方程式を漸化式に置き換えることで、音や画像のフィルタリングを実現します。音声エフェクトやノイズ除去、画像のぼかしや輪郭抽出も、根底にはこの変換の数理が息づいています。
つまり、私たちの身の回りのデジタル技術の多くは、「微分を漸化式で再現する」ことによって成立しているのです。スマートフォンで再生される音楽や、AIによる画像生成の背後にも、連続と離散を結ぶこの橋が静かに流れています。
次章では、こうした応用の先にある哲学的な意義——なぜ人類は「変化」を記述することにこれほど惹かれてきたのか——について考えてみましょう。
社会的意義・未来の展望:離散と連続の調和が導く未来
デジタル時代における「離散の勝利」
現代社会は、ほとんどあらゆるものがデジタル化されています。写真、音楽、言語、映像、通貨、さらには思考の断片までもが、0と1という離散的な情報単位に変換され、ネットワークを流れています。私たちは無意識のうちに、漸化式的な世界——一歩ごとの更新と演算の繰り返し——の中で暮らしているのです。
このような離散的処理の中で、かつて連続的にしか表せなかった現象が「近似」として再現されています。ディスプレイの滑らかな映像も、マイクロ秒単位で変化する音の波も、実際には微小なステップで計算された結果です。つまり、漸化式は現代文明の根底で、世界の模倣者として機能しているのです。
連続の再発見:AIと自然の融合
一方で、AIや機械学習の進化によって、私たちは再び「連続性」の力を再発見しています。ニューラルネットワークの重みは、連続的な関数空間の中で変化し、微分によってその最適化が導かれます。デジタル計算機の内部であっても、思想としては「滑らかに変化する世界」を模倣しているのです。
この融合は、まるで古代ギリシアの哲学者たちが夢見た「数による自然の理解」が、現代の形で実現しつつあるように見えます。離散的なアルゴリズムと連続的な解析が、互いの限界を補い合いながら、ひとつの知的体系を形成し始めています。
数学が示す哲学的メッセージ
漸化式と微分の関係は、単なる技術的対応を超えて、人間の思考の二面性を象徴しています。私たちは「段階的に考える」存在であると同時に、「全体を滑らかにとらえる」存在でもあります。つまり、離散と連続は「人間の知の構造」そのものに対応しているのです。
漸化式的な思考は、「いま何をすべきか」という行動の連鎖を導きます。微分的な思考は、「この変化がどこへ向かうのか」という全体像を示します。現代の社会問題や技術的課題においても、この二つの視点が欠けると、理解は断片的になります。数学は、そのことを静かに教えてくれるのです。
未来への視座:離散と連続の統合
未来の科学・技術は、この二つの世界をより自然に統合していくでしょう。量子コンピュータのアルゴリズムや、連続的な空間を離散的な情報として圧縮する生成AI、あるいは自然現象のシミュレーション技術——それらはすべて、漸化式と微分の架け橋の上に築かれています。
離散は精密な構造を与え、連続は滑らかな意味を与える。両者が共存することで、計算と創造の境界が曖昧になり、新しい「知の地平」が開かれるのです。もしかすると、私たちが目指す人工知能とは、まさに「離散と連続の融合する意識」なのかもしれません。
漸化式と微分の物語は、数学史の一章にとどまらず、人類が世界をどうとらえるかという根源的な問いを映し出しています。次章では、その哲学的な意味をふまえ、私たちがこの数理の二つの世界から学べることをまとめていきます。
まとめ・結論:変化をとらえる二つのまなざし
漸化式と微分——この二つの数学的手法は、離散と連続という世界の二つの見方を象徴しています。漸化式は「一歩先」を知るためのルールであり、微分は「今この瞬間」を解析するための道具です。どちらも「変化を記述する」という一点で深く結びついており、視点の違いこそがそれぞれの力を生んでいます。
漸化式の本質は「生成」にあります。時間を細かく刻みながら、未来を少しずつ構築していく。これは人間の思考や学びのプロセスにも似ています。一方、微分の本質は「洞察」にあります。全体を見渡し、変化の傾向や法則を読み解く。これは直観的理解や創造に通じる行為です。
現代社会では、離散的なデジタル技術と、連続的な自然現象とが絶えず交差しています。コンピュータは漸化式のように反復的に世界を計算し、AIは微分のように滑らかに最適解を探ります。つまり、私たちが使うあらゆるテクノロジーの背後に、「漸化式と微分」という双子の原理が息づいているのです。
そしてこの二つは、単なる数学的概念にとどまりません。それは「時間をどう感じるか」「世界をどう構築するか」という、哲学的な問いへのヒントでもあります。私たちは、一瞬一瞬を積み重ねる離散的な存在でありながら、その流れ全体を意味としてとらえる連続的な意識をもっています。数理の世界に見える調和は、人間存在そのものの構造にも通じているのです。
漸化式と微分の間を行き来すること——それは、計算と直観、部分と全体、有限と無限の間を往復することでもあります。その往還のなかでこそ、真の理解と創造が生まれます。変化を恐れず、その構造を見つめ、次の一歩を導くこと。それが、この数理的思考が私たちに与えてくれる最大の贈り物なのかもしれません。
離散と連続、計算と洞察。そのあいだにある静かな橋を渡るとき、数学は単なる知識を超え、ひとつの「生き方の比喩」となります。世界の変化を感じ取りながら、自らも変化していく——それが、漸化式と微分が教えてくれる、普遍的な生のリズムなのです。

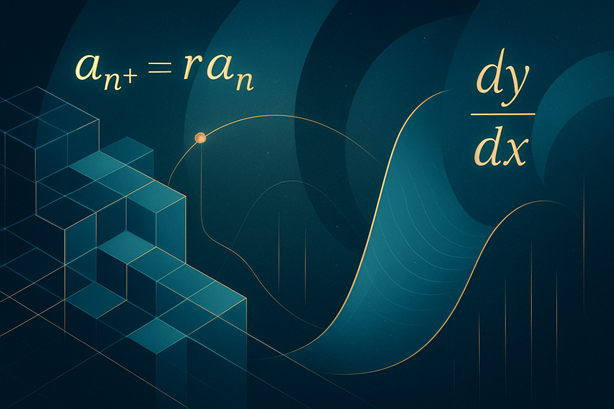
コメント