① 導入・背景:波の奥にひそむ“かたち”を読み解く道具
私たちが生きる世界は、静止しているように見えて、常にゆらぎ、動き、変化しています。空気の震えが音となり、光の波が色を生み、株価の上下が社会の動きを映し出す──。これらは一見、複雑でバラバラな現象のように見えますが、実はどれも「時間とともに変化する信号」として捉えることができます。
そして、その信号の奥に潜む本質を読み解くための“鍵”が、「フーリエ変換」です。
フーリエ変換とは、複雑な波や信号を「どのような成分が、どれくらいの割合で含まれているのか」という“周波数の言葉”に翻訳する数学的な道具です。たとえば、ギターの音は一本の弦が振動しているだけのように聞こえますが、実際には複数の周波数の波が重なり合ってできています。フーリエ変換を使えば、その音がどんな高さの音(周波数)で構成されているかを分解して知ることができます。これは、音だけに限りません。光のスペクトル解析、画像の特徴抽出、心電図の解析、通信信号の復元──その応用は科学・技術のあらゆる領域に広がっています。
ではなぜ、わざわざ「周波数の世界」に変換する必要があるのでしょうか。
それは、時間のままでは見えにくい“本質”が、周波数の視点に立つことで鮮やかに浮かび上がるからです。時間軸では雑多に見える波の形も、周波数軸で見ると秩序ある構造として現れます。まるで、複雑な和音を一音一音に分解するように、現象の「構成要素」が見えてくるのです。
現代社会は、この「見えない構造を読み解く力」に大きく依存しています。スマートフォンで音声通話ができるのも、インターネットで膨大なデータをやり取りできるのも、医療機器が人体の情報を解析できるのも、その根底にはフーリエ変換の考え方があります。つまり、フーリエ変換は単なる数学の一手法ではなく、「変化を分解して理解する」という人類の知的戦略そのものなのです。
この記事では、このフーリエ変換を、数式ではなく“考え方”から丁寧に解きほぐしていきます。どのような仕組みで動いているのか、なぜそれほど重要なのか、そしてそれが未来にどのような可能性を切り拓くのか──。私たちが日々触れているあらゆる「波」を読み解く旅の入口として、その背景と本質を探っていきましょう。
② 基礎解説・前提知識:波を「足し合わせて理解する」という発想
フーリエ変換の本質を理解するためには、まず「波とは何か」「なぜ波を分解するのか」という基本的な考え方から整理する必要があります。ここでは、数式ではなく“直感”でその原理に近づいてみましょう。
● 世界は「波」でできている
音、光、電波、地震の揺れ、人間の脈拍──これらは一見バラバラな現象に思えますが、すべて「時間とともに変化する量」、つまり「波」として表すことができます。
波とは、時間の経過に応じて繰り返し変化するパターンのことです。もっとも基本的な波は「正弦波」と呼ばれ、なめらかな上下運動を繰り返します。音叉を鳴らしたときの音、太陽光の色を構成する光の振動、心臓の拍動のグラフ──これらも、根本的には「正弦波の組み合わせ」で説明できるのです。
● 複雑な波は「単純な波の足し算」でできている
ここで、非常に重要な考え方があります。それは、「どんな複雑な波でも、単純な正弦波をたくさん足し合わせることで表現できる」というものです。
たとえば、ギターの音は決して単純な波ではありませんが、ある高さの音(低周波)、その倍の高さの音(倍音)、さらにそのまた倍の音……といった複数の正弦波を重ねることで、ほぼ同じ波形が再現できます。これは「フーリエ級数」と呼ばれる考え方で、フーリエ変換の土台となっています。
この「分解して足す」という発想は、自然界の多くの現象にも通じています。白い光は、赤・緑・青といった複数の色の光が重なったものですし、複雑な香りは多様な分子の組み合わせでできています。同じように、複雑な波も“単純な波の集合体”として見ることができるのです。
● フーリエ変換とは「波の中身を調べる道具」
このような前提のもとで、フーリエ変換が何をしているかを簡単に言うと、「ある信号にどの周波数の波が、どれくらい含まれているかを調べる」という操作です。
これを音の例で考えてみましょう。
ある録音データがあるとき、それを時間のまま見ると「波がぐちゃぐちゃしているな」としか分かりません。しかし、フーリエ変換を行うと「100Hzの成分が強く、200Hzと300Hzも少し含まれている」といった“周波数ごとの構成”が明らかになります。つまり、時間軸で見ていたデータを「周波数軸」というまったく別の視点に変換することで、その本質的な構造を読み解けるようになるのです。
このとき得られる結果は「スペクトル」と呼ばれます。スペクトルは、どの周波数がどれくらい強く含まれているかをグラフで表したもので、音の特徴、画像のパターン、信号の性質などを一目で把握することができます。
● 周波数とは「時間の裏側の情報」
ここで登場する「周波数」という言葉を、もう少し丁寧に見ておきましょう。
周波数とは、「1秒間に何回繰り返すか」という数値です。たとえば1秒間に440回振動する音波は、440Hz(ヘルツ)の音と呼ばれます。高い音ほど周波数が大きく、低い音ほど周波数は小さくなります。
重要なのは、周波数が単なる数値ではなく「時間の裏側の情報」であるという点です。時間軸では“いつどのように変化したか”が分かりますが、周波数軸では“どんな性質の変化が含まれているか”が分かります。この2つは表裏一体の関係であり、フーリエ変換はその橋渡しをしてくれるのです。
● 時間の世界から周波数の世界へ
ここまでをまとめると、フーリエ変換は次のようなステップで世界を読み解いています。
- 複雑な波は、単純な波(正弦波)の足し算でできている。
- その「足し算の内訳」を調べるのがフーリエ変換である。
- それにより、時間の世界では見えなかった構造が、周波数の世界で明らかになる。
この視点の切り替えは、数学的なテクニックであると同時に、ものの見方そのものを変える思考法です。時間軸では見通せなかった現象が、周波数軸では規則正しい構造として現れる──この“見え方の転換”こそが、フーリエ変換が単なる計算手法を超えて、自然や情報の本質を解き明かす強力な道具として機能している理由なのです。
③ 歴史・文脈・発展:熱から生まれた“波の言語”
フーリエ変換の物語は、実は「熱」という一見単純な現象から始まりました。19世紀初頭、フランスの数学者ジョゼフ・フーリエは、金属棒の中をどのように熱が伝わっていくのかという問題に挑んでいました。彼は温度の分布を関数で表し、その変化を解こうとしましたが、現実の関数は複雑で解析が困難でした。そこで彼が思いついたのが、「複雑な関数を単純な波の足し算として表す」という大胆なアイデアでした。
彼の考えはこうです。どんな複雑な周期的な現象も、無数の正弦波と余弦波の重ね合わせで表現できる。この考え方は「フーリエ級数」と呼ばれ、後のフーリエ解析の基礎となりました。式で書けば次のようなものです:
f(t) = a0/2 + Σ [ an cos(nω0t) + bn sin(nω0t) ]
ここで ω0 は基本周波数、an・bn はそれぞれの波の強さを表します。フーリエの主張は、当時の数学界ではあまりに革命的で、多くの批判を浴びました。不連続な関数までこの方法で表せるという点は、とくに直感的に受け入れられなかったのです。
数学界の論争と理論の成熟
それでも、彼の発想は後に大きな転換点となりました。ラグランジュやポアソンといった数学者たちとの激しい議論の末、関数論と解析学の新しい枠組みが整備され、フーリエ級数は次第に受け入れられていきます。19世紀中頃には、ダルブーやリーマンらの研究によって理論が厳密化され、「複雑な現象は単純な波の和で表せる」という考えは数学の中心概念のひとつとなりました。
周期から非周期へ ― フーリエ変換の誕生
しかし、この手法には限界もありました。それは「周期的な現象」にしか使えないという点です。自然界の多くの信号──たとえば音声、地震波、株価データなど──は、周期的ではありません。そこで登場するのが、現代でいう「フーリエ変換」です。これは、周期を仮定せず、信号を連続的な周波数成分へと展開する手法です。
フーリエ変換は次のように表されます:
F(ω) = ∫ f(t) e-iωt dt
f(t) = (1 / 2π) ∫ F(ω) eiωt dω
この考え方によって、時間的には一度きりの現象でも、その中に含まれる周波数の構成要素を詳細に分析できるようになりました。これは、自然界のあらゆる信号解析を可能にする強力なツールとなり、フーリエ解析は数学を超えて工学、物理学、通信といった応用分野へと一気に広がっていきます。
工学と科学への波及 ― 波動と信号の時代へ
19世紀後半には、電磁気学の父・マクスウェルが電磁波の理論にフーリエ解析を用い、20世紀に入ると量子力学でも波動関数の解析に使われるようになりました。さらに通信技術が発展すると、信号を周波数ごとに処理する考え方は欠かせないものとなり、ラジオや電話、インターネットといった技術の根幹を支える存在となります。
計算革命 ― FFTの登場とデジタル時代
そして20世紀後半、この分野にもう一つの革命が訪れます。それが「高速フーリエ変換(FFT)」の登場です。1965年、クーリーとトゥーキーが発表したアルゴリズムは、従来では膨大な計算量が必要だったフーリエ変換を劇的に高速化しました。これにより、音声や画像のリアルタイム処理が可能となり、デジタル信号処理の時代が到来します。
今日、フーリエ変換は私たちの生活のあらゆる場面に潜んでいます。スマートフォンの通信、音楽の圧縮、医療機器の解析、天文学の観測──そのどれもが、フーリエが200年前に見出した「複雑な現象を単純な波に分解する」という考え方の延長線上にあります。彼のアイデアは、単なる数学的手法を超えて、「世界の見方」そのものを変えたと言えるでしょう。
④ 応用・実例・ケーススタディ:見えない構造を“読み取る”技術へ
フーリエ変換は、単なる数学の一手法ではありません。それは、現代社会のあらゆる技術の「中枢神経」のような存在です。音声・画像・通信・医療・地球科学など、異なる分野に共通して使われる理由は、「複雑なデータの中から、本質的な構成要素を抽出できる」からです。ここでは、具体的な応用例を通して、その力を見ていきましょう。
● ① 音の世界を“分解”する ― 音声解析と楽器の波形
もっとも身近な応用のひとつが、音声や音楽の解析です。私たちが耳で聴いている音は、時間とともに複雑に変化する波形ですが、それをフーリエ変換すれば「どの周波数が、どれだけ含まれているか」が一目でわかる「スペクトル」として可視化できます。
たとえば、ギターの弦をはじいたときの音は、基本の周波数(基音)とその倍数の周波数(倍音)で構成されています。スペクトル解析を行うと、これらの倍音の強さや位置がグラフとして現れ、楽器の「音色」の違いまで読み取ることが可能になります。
さらに、音声認識の分野では、人間の声を周波数成分に分解し、母音や子音の特徴を抽出して文字情報へと変換する技術にも利用されています。SiriやGoogle音声アシスタントが私たちの声を理解できるのは、このフーリエ解析が根底で動いているからです。
● ② 見えない世界を見る ― 画像処理とコンピュータビジョン
フーリエ変換は「音」だけでなく、「画像」にも応用されます。画像を二次元信号とみなし、フーリエ変換を行うと、空間のパターンが「周波数成分」として表現されます。
この特性は、画像のノイズ除去やシャープ化、圧縮などに広く使われています。たとえば、写真から不要なノイズを取り除く場合、高周波成分(細かい変化)を抑えることで滑らかな画像を得ることができます。一方、エッジ検出や特徴抽出では逆に高周波成分を強調するなど、目的に応じて「周波数空間での操作」が行われます。
また、近年では顔認識や自動運転カメラの画像解析にもフーリエ変換が活用されています。画像全体を時間軸で見るのではなく、「構造のパターン」として読み取ることで、AIはより効率的に特徴を抽出し、判断を下せるのです。
● ③ 情報を正確に届ける ― 通信とデータ圧縮
スマートフォンで動画を見たり、Wi-Fiでインターネットにつながったりできるのも、フーリエ変換の力によるものです。通信分野では、信号を周波数成分に分解して送受信する技術が基本となっています。
たとえば、無線通信では「直交周波数分割多重(OFDM)」という方式が使われます。これは、ひとつの大きな信号を複数の周波数帯に分けて並列で送信する仕組みで、フーリエ変換が欠かせません。
また、音声や映像の圧縮技術でも、フーリエ変換が活躍します。MP3やJPEGといったフォーマットは、信号を周波数成分に分解し、人間の感覚に不要な要素を間引くことでデータ量を大幅に削減しています。
つまり、私たちが毎日使っている通信・ストリーミング・SNSの基盤は、「波を分解して効率的に扱う」というフーリエの思想に根ざしているのです。
● ④ 体の中の“信号”を読む ― 医療と生体解析
医療の現場でも、フーリエ変換は欠かせません。代表的な例が心電図(ECG)や脳波(EEG)の解析です。これらの波形データは複雑で一見読み解くのが難しいですが、フーリエ変換を用いれば異常な周波数成分を検出でき、病気の早期発見につながります。
さらに、MRI(磁気共鳴画像)にもフーリエ変換が応用されています。MRIは体内からの信号を周波数空間で記録し、それを逆フーリエ変換して画像として再構成します。つまり、私たちが目にしている「体内の断層画像」は、フーリエ解析によって“波の情報”から復元されたものなのです。
● ⑤ 地球規模の応用 ― 地震・天文学・AIへ
応用の範囲は、地球規模にも広がっています。地震波解析では、地中を伝わる複雑な振動を周波数解析することで、震源や地層構造を推定します。天文学では、星の光のスペクトルを解析して化学組成や運動を調べることが可能です。
さらに、近年注目されているのが、AI・機械学習分野での利用です。ディープラーニングでは、データの前処理としてフーリエ変換を用いることで、パターン認識の精度を高める手法が登場しています。これは、AIが「時間」ではなく「構造」を理解するための前処理とも言えます。
● 「構造を見る」力が未来を支える
このように、フーリエ変換は「音を聴く」「画像を見る」「信号を送る」「体を診る」といった多様な分野で活躍しています。そのどれもに共通しているのは、「時間軸で複雑な現象を、周波数軸で単純な構造として捉え直す」という本質的な考え方です。
私たちは普段、変化を“時間”という直線の中でしか見ていません。しかし、フーリエ変換はそれを“周波数”というもう一つの空間に引き出し、見えなかった秩序や特徴を浮かび上がらせてくれます。その視点の転換こそが、現代社会の技術革新の土台となっているのです。
⑤ 社会的意義・未来の展望:波を読む力が、世界の未来を形づくる
フーリエ変換は、今や科学や工学の枠を超え、「現代社会の知的インフラ」と呼べるほどの存在になっています。スマートフォンの通信から医療診断、AIの学習、気候予測、宇宙探査まで──目に見える成果の背後では、常に“波を読み解く”技術が働いています。しかし、それは単なる便利な道具という意味にとどまりません。フーリエ変換は、私たちが「世界の構造をどう捉えるか」という思考そのものを変えつつあるのです。
● 情報社会の「翻訳装置」としての意義
21世紀は「情報の時代」と言われますが、その情報の多くは、時間の中で絶えず変化する“信号”として存在しています。人間の声、映像、株価、気象データ、センサーからの出力──それらはすべて時間の連続として流れてきます。
しかし、人間もAIも、生の信号のままではその本質を理解することができません。そこで必要になるのが、「別の言語」への翻訳です。フーリエ変換は、まさにその役割を担います。
時間という雑多な言語を「周波数」という整理された言語に翻訳することで、私たちは情報の本質を把握し、制御し、活用できるようになります。この“翻訳装置”としての役割は、今後、データ量と複雑性が爆発的に増大する未来社会において、ますます重要性を増していくでしょう。
● AI・機械学習との融合 ―「特徴」を読む力へ
近年、フーリエ変換の価値は新しい局面に入っています。それは、AIや機械学習との融合です。
AIがデータを学習する際、最も重要になるのは「特徴の抽出」です。つまり、膨大なデータの中から「意味のあるパターン」を取り出すことが鍵となります。ここでフーリエ変換は、時間や空間の表現を“構造”として読み解く強力な手段となります。
たとえば、音声認識AIでは、生の波形をそのまま入力するのではなく、フーリエ変換を使って周波数スペクトルへと変換し、そこから特徴を学習します。画像解析でも、空間的な特徴を抽出するために周波数空間での処理が行われます。
今後、AIが人間を超えるパターン認識力を発揮するためには、この「波の言語」を自在に操る能力が不可欠になると考えられています。
● 新しい科学の地平 ― 複雑系・量子・宇宙へ
フーリエ変換の応用は、既存の工学を超えて、科学の根本的な探究へと広がっています。
たとえば、地球規模の気候変動や経済システムのような「複雑系」では、膨大な時系列データの背後に潜むリズムや周期性を見つけることが重要です。フーリエ解析は、その“隠れた秩序”を浮かび上がらせる道具として、シミュレーションやモデル化の基盤となっています。
さらに、量子物理学の世界でも、波動関数の解析やスペクトルの測定にフーリエ的な手法が用いられています。宇宙科学においては、星の光のスペクトル解析や重力波の検出など、宇宙の「音」を聴き取る技術として欠かせません。
このように、フーリエ変換は“ミクロの世界”から“宇宙の果て”まで、自然現象を読み解く普遍的な方法論として進化を続けているのです。
● 社会構造の可視化 ― 人間の行動を“波”として捉える
面白いことに、フーリエ変換の応用は自然科学だけにとどまりません。近年では、社会科学や経済学の分野でも注目されています。
人々の購買行動やSNS上の発言の増減、交通量の変化なども、時間とともに変化する「社会の波」として捉えることができます。周期的なトレンドや季節性、突発的な変化などを周波数の観点から分析することで、政策立案やマーケティング、危機管理などに活かす試みも始まっています。
これは、私たちが「社会」そのものを“波”として見るという新しい視点を得たことを意味します。フーリエ変換は、技術を超えて、社会の構造や人間の行動の「読み解き方」そのものに影響を与えつつあるのです。
● 見えない構造を見抜く“知性”へ
これからの時代、情報はますます複雑化し、変化はさらに加速していきます。そうした中で求められるのは、表面に現れた現象だけでなく、その背後にある「構造」を見抜く知性です。フーリエ変換は、その知性を支える最も根本的な技術のひとつといえるでしょう。
200年前、フーリエは「熱」という一見単純な現象の奥に、波としての構造を見出しました。そして今日、私たちはあらゆる現象の背後に「波」を見ています。これは単なる数学の発展ではなく、人類の“認識の進化”でもあります。
未来の科学・技術・社会は、この「波を読む力」をどこまで深められるかによって、その可能性が決まっていくと言っても過言ではありません。
⑥ 議論・思考・考察:世界は“足し合わせ”でできているという視点
フーリエ変換は、表面的には単なる数学的な道具のように見えます。しかし本質的には、それ以上のものです。それは「世界の見方」を根本から変える思考法であり、複雑な現象を理解するための“哲学”でもあります。この章では、その深層にある意味を、数式の外側から見つめ直してみましょう。
● 分解することは「理解すること」
フーリエ変換の基本的な考え方は、非常にシンプルです。「複雑なものは、単純な要素の組み合わせとして表せる」という原則。この発想は、科学の根本原理のひとつと言ってよいでしょう。
たとえば、化学では物質を元素に分解して理解します。言語学では文章を文法構造に分解し、音楽では和音を単音に分解します。どの分野でも、「全体をそのまま眺めているだけでは本質はつかめず、構成要素に分けてはじめて理解が進む」のです。
フーリエ変換はその“分解”を時間や空間の領域で行う道具であり、複雑な信号や現象の背後にある構造を明らかにします。これは単なる技術的操作ではなく、「理解とは何か」という問いに対する一つの答えでもあるのです。
● 世界は「和」でできているという認識
フーリエ変換の思想が深いのは、「すべての複雑さは“和”によって成り立っている」と教えてくれる点です。
音も光も、社会の動きも、単一の原因ではなく、無数の要素が重なり合い、干渉し合い、全体としての形を成しています。たとえば、ニュースで報じられる経済の動きも、個々の人々の行動、企業の判断、自然の変動など、さまざまな“波”の重ね合わせの結果です。
この視点を持つと、私たちのものの見方も変わります。目の前の現象を「一つのもの」として捉えるのではなく、「複数の成分の調和として存在している」と見るようになるのです。これは科学だけでなく、人間関係や社会問題の理解にも応用できる考え方です。表面的な“結果”だけを見るのではなく、“構成”に目を向けることが、より深い洞察へとつながります。
● 「時間」だけでは見えないもの
フーリエ変換の根底にあるもう一つの思想は、「同じ現象でも、別の見方をすれば違う姿が見える」ということです。
時間の中で見ると複雑で予測不能に思える波も、周波数という軸に変換すれば、規則的で単純な構造として姿を現します。この「視点の転換」は、科学の歴史において繰り返し重要な意味を持ってきました。
ニュートンは運動を「力」という概念で捉え直し、ダーウィンは生命の多様性を「進化」という枠組みで見直しました。フーリエは、時間的な現象を「周波数」という別の次元で読み解く道を開きました。視点を変えるだけで、同じ世界がまったく違って見えてくる──その事実自体が、フーリエ変換の最大の示唆かもしれません。
● 「複雑さ」と「単純さ」は対立しない
現代社会は、かつてないほど複雑化しています。膨大な情報、複雑な経済構造、入り組んだ人間関係。私たちはしばしば、その複雑さに圧倒され、「全体像を理解することは不可能だ」と感じます。
しかしフーリエ変換は、その考え方に一石を投じます。
複雑なものも、単純なものの集まりとして見れば理解できる。全体をそのままではなく、要素ごとに捉えれば、秩序を見出せる。
この「複雑さと単純さは対立しない」という考え方は、科学だけでなく、私たちの思考法にも応用できます。たとえば、大きな問題に直面したとき、すべてを一度に解決しようとするのではなく、「構成要素」に分けて一つずつ解きほぐしていく──それが本質に近づく道筋なのです。
● “分解”の先にある“再構成”
最後にもう一歩踏み込むと、フーリエ変換の本質は「分解」そのものではなく、「分解と再構成の往復」にあります。
波を周波数成分に分けることは、理解への第一歩にすぎません。そこからどの要素が重要なのか、どれを強調し、どれを削ぎ落とすかを考え、再び全体像を組み立て直す――これこそが、知性の本領です。
この“再構成”という視点は、創造の領域にも通じています。音楽家は音を分解して理解した上で、新たな旋律を生み出します。科学者は現象を分析して要素を見極め、新しい技術を設計します。人間の知性は、分解と再構成のサイクルの中で進化してきたのです。
● 波の哲学としてのフーリエ変換
フーリエ変換は、単なる計算手法ではありません。それは「複雑なものは分解できる」「見方を変えれば新しい構造が見える」「全体は部分の和である」という、世界を読み解くための哲学的なレンズです。
そしてこのレンズは、情報や技術の未来だけでなく、私たちの思考、創造、そして生き方そのものにまで影響を与えています。
世界を“波”として見る。
それは、表面の現象の背後に潜む構造を感じ取り、複雑さの中に秩序を見出す知性の行為です。フーリエ変換とは、そうした「見る力」を私たちに与えてくれる、人類の思考装置なのです。
⑦ まとめ・結論:波の中に、世界の秩序を読み解く
フーリエ変換とは何か――。それは、単なる数学的な変換式ではありません。私たちが日々触れているあらゆる現象の背後に潜む「構造」を、見える形で引き出すための“思考の道具”です。
音や光、通信やデータ、脳波や地震波といった多様な現象は、一見するとまったく別のもののように思えます。しかし、時間の流れとともに変化する「波」という共通の姿に還元できる。そして、その波を「どの成分で構成されているか」に分解し、理解し、再構築すること――それこそがフーリエ変換の本質です。
● 世界を「時間」から「構造」へと翻訳する
フーリエ変換の最大の意義は、時間という表面的な軸を超えて、物事の本質的な構造を明らかにできる点にあります。
時間軸では雑多で複雑に見える現象も、周波数という別の軸に変換すれば、規則的で秩序だった姿を見せます。それは、まるで混ざり合った音楽を一音ずつに分けて聴くような体験です。
この「見方の転換」は、技術的な利便性を超えて、私たちの認識そのものを深める行為でもあります。世界は、ただ時間の中で流れているのではなく、無数の成分の“和”として構成されている――フーリエ変換はその事実を教えてくれるのです。
● 技術の核心として、思考の原理として
現代社会のあらゆる技術は、この「波の言語」を基盤に成り立っています。音声認識、画像解析、通信、医療、AI、気候予測、宇宙観測――そのどれもが、フーリエ変換によって複雑なデータを読み解き、構造化し、活用しています。
しかし同時に、フーリエ変換は技術のためだけのツールではありません。それは「複雑なものを単純な要素に分けて考える」「別の次元から世界を見る」という、人間の知性の本質的な思考法を体現しています。この原理は科学だけでなく、社会や人生の理解にも応用できる普遍的な洞察です。
● 波の向こうにある未来へ
これからの時代、データはますます膨大になり、現象はさらに複雑になります。AIが進化し、量子コンピュータが登場し、人間社会そのものがダイナミックに変動するなかで、「本質を見抜く力」はこれまで以上に重要になるでしょう。
フーリエ変換は、その時代においても色あせることのない思考の核です。単なる数式ではなく、「世界を分解し、構造として再構成する」ための知性の道具として、今後も科学と社会の両面で不可欠な役割を果たしていくはずです。
● 結びに ― 見えない秩序を見抜く目
フーリエが200年前に発見したのは、単なる数学的な手法ではありません。それは、「見えないものを見えるようにする方法」そのものでした。
世界の複雑さに圧倒されたとき、私たちはフーリエ変換の思想に立ち返ることができます。つまり、「どんな複雑な現象も、要素の重ね合わせとして読み解ける」という視点です。
この視点を手にすることは、科学者にとっても、技術者にとっても、そして日常の中で世界を理解しようとする私たち一人ひとりにとっても、大きな力となります。
フーリエ変換――それは、波の奥に潜む秩序を見抜き、複雑さの中に構造を見出すための、最も根源的な知の道具なのです。
📊 追記:時間と周波数、二つの“世界”から見る鐘の音
最後に、フーリエ変換の本質をもっと直感的に理解するために、「鐘の音」を時間軸と周波数軸の両方から眺めてみましょう。これまでの解説が、どのような“現実”とつながっているかが実感できるはずです。
① 時間の世界:波の「物語」を見る
下の図は、鐘の音を録音して時間軸上に描いた「波形(waveform)」です。最初に大きな衝撃があり、その後、小さな波が続きながらゆっくりと消えていく様子がはっきりと見えます。これは、耳で聞こえる「ゴーン……」という音そのものを可視化したものです。
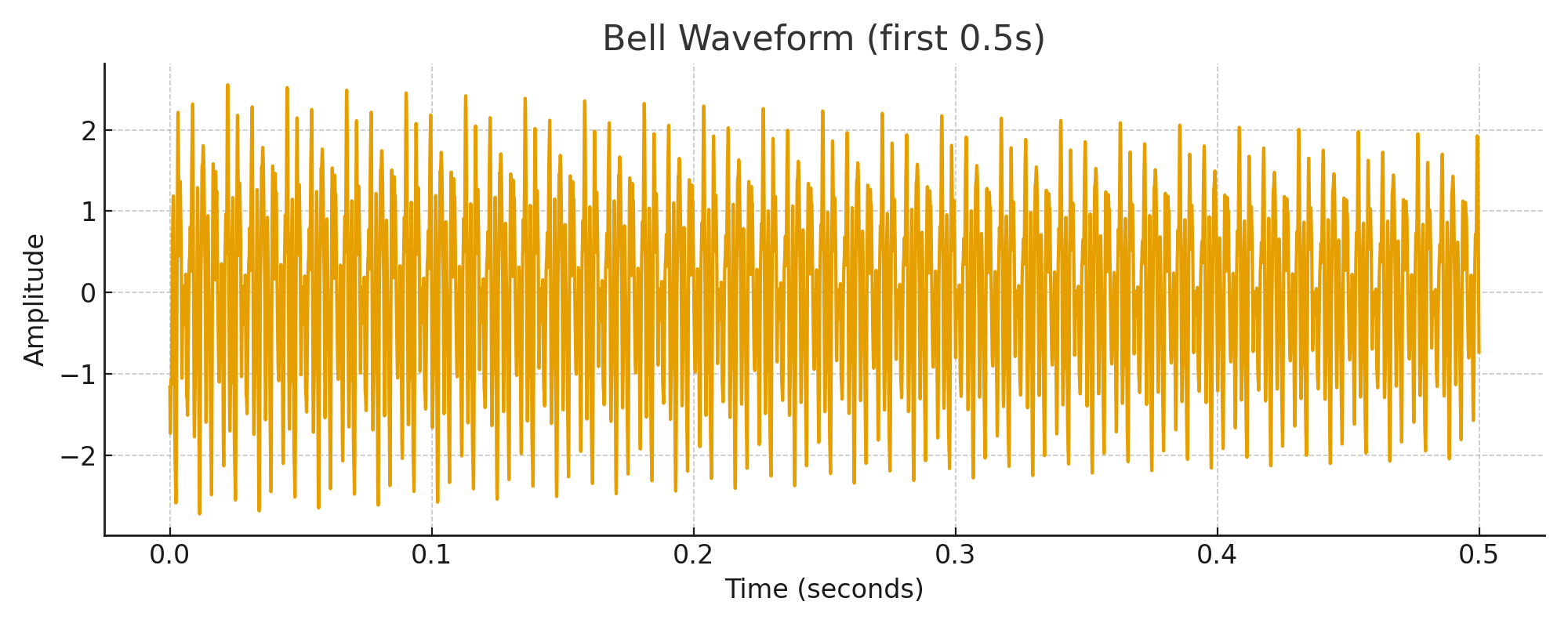
この図だけでは、「どの周波数が鳴っているのか」は読み取れません。しかし、“音がどのように始まり、どのように変化し、どのように消えていくか”という時間的な特徴が一目でわかります。これは、音の“物語”を見る視点です。
② 周波数の世界:音の「構造」を見る
次の図は、同じ鐘の音をフーリエ変換して得られた「スペクトル(spectrum)」です。縦軸は音の強さ、横軸は周波数を表しており、音に含まれる“成分”がどこに存在しているかがわかります。
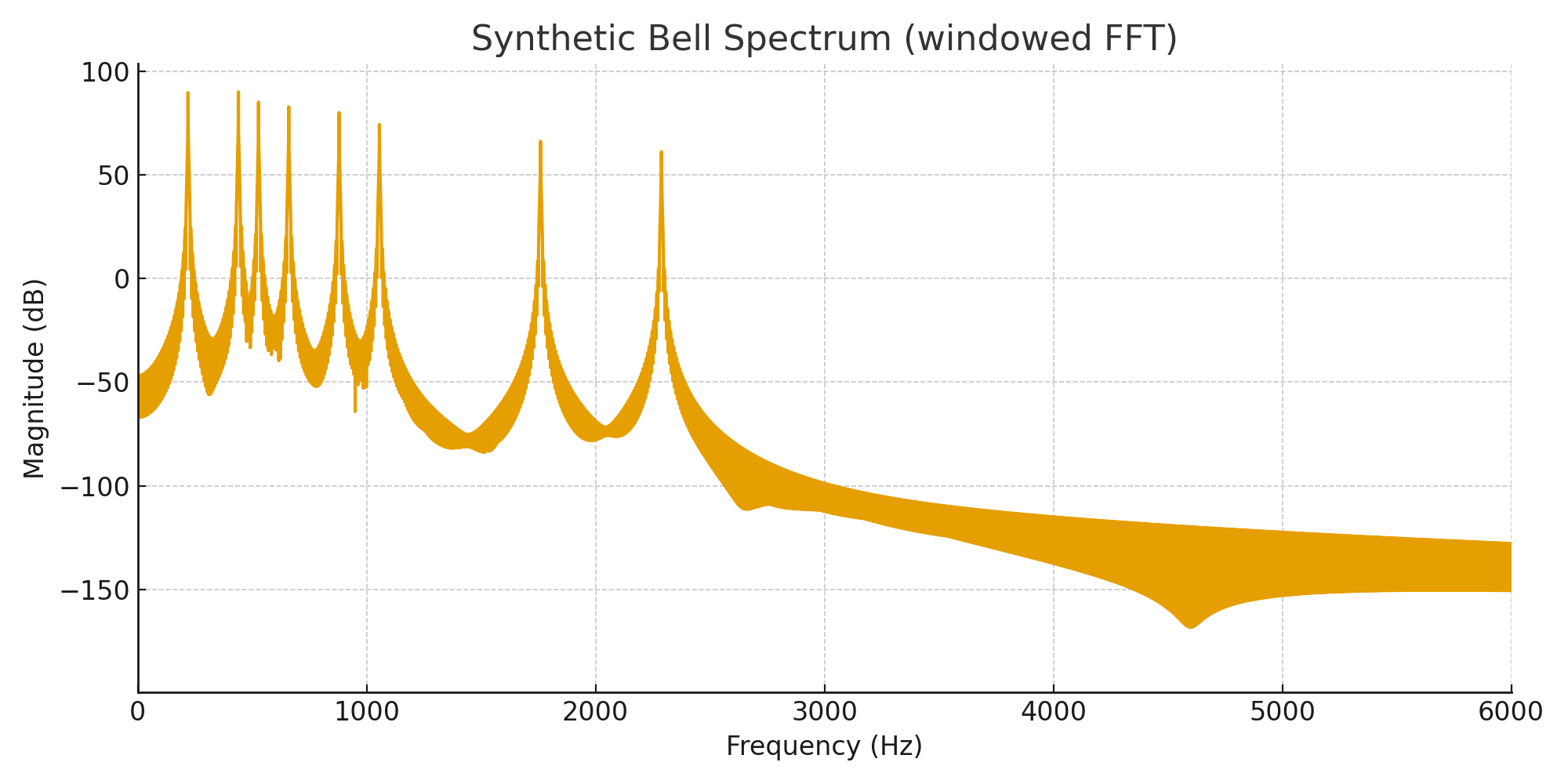
時間波形ではただの「ゴーン」という音にしか見えなかったものも、周波数の世界では複数の音が重なり合う“合奏”であることが見えてきます。これが、フーリエ変換の最大の魅力です。
※ここで示しているスペクトルは、鐘の音全体(約3秒間)のデータをまとめて解析したものです。時間のどの瞬間かという情報は含まれておらず、「この鐘という音には、どのような周波数成分がどれくらい含まれているか」という“特徴”だけを示しています。
一方で、波形は時間とともに音がどのように変化していくかを表したものであり、0.5秒という短い区間を切り出して詳しく見ています。このように、波形とスペクトルは「時間の変化」と「音の中身」という異なる側面を示すものであり、両方を合わせてはじめて鐘の音の全体像が見えてくるのです。
③ 二つの世界をつなげる「視点の変換」
時間の波形と周波数のスペクトルは、同じ音の「二つの顔」です。波形は音のストーリーを語り、スペクトルはその構造を示します。フーリエ変換は、この二つの視点を行き来する“翻訳装置”のようなものです。
鐘の音だけでなく、心臓の鼓動も、地震波も、株価も、すべては時間の中に流れる「波」です。そして、それを分解して本質を読み解くとき、私たちはその背後にある秩序や構造を初めて“見る”ことができるのです。
フーリエ変換の“周期性”という考え方は、実は自然対数とも深く関係しています。 その関係をもう少し数学的に整理したのが、こちらの記事です → 自然対数とは何か


コメント