私たちは日常のなかで、数という概念に無意識のうちに囲まれて生きている。お金の計算からスマートフォンの電池残量、人口統計、気温の変化まで、数は世界を測るための共通言語だ。その中でも、整数や分数、円周率や平方根といった有名な数は、多くの人にとって馴染み深い存在だろう。しかし、数学の世界には「自然対数」と呼ばれる、少し特別な“数の流儀”がある。聞き慣れない言葉かもしれないが、この概念は科学・技術・自然現象の根幹に静かに息づいており、私たちの生活の背後で大きな役割を果たしている。
自然対数とは、端的にいえば「自然な増え方」を記述するための数の体系だ。成長・減衰・変化といった時間とともに起こる現象は、しばしば直線的ではなく、指数的なカーブを描く。たとえば人口が増えるスピード、ウイルスが拡大する勢い、銀行の複利計算、放射性物質の減衰、さらには株価の長期的な推移までもが、指数的な法則に従っている。こうした世界を正確に表現するために、数学者たちが見出したのが「自然対数」であり、そこに現れる特別な定数が「e」という数である。
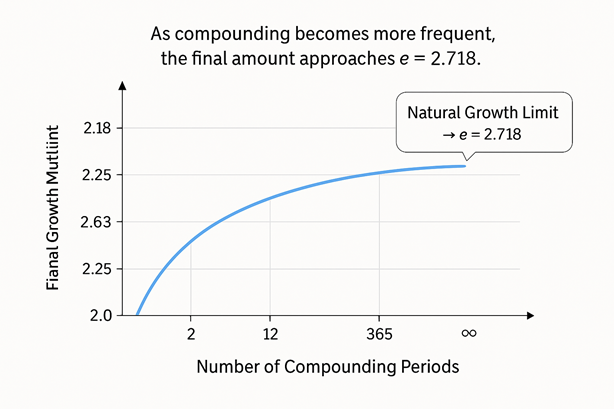
「e」はおよそ 2.71828… という無限に続く小数であり、円周率 π と並ぶ“自然界の根源的な定数”と称される。円周率が円の性質から必然的に導かれるように、「e」は増殖や変化といったダイナミズムの中から自然に現れる。興味深いのは、この数が誰かが恣意的に作り出したものではなく、あらゆる現象の根底から「勝手に」顔を出してくるという点だ。まさに“自然”という名が冠される所以である。
現代社会においても、自然対数は思いがけないほど広範囲に応用されている。コンピュータのアルゴリズム解析、確率論や統計学の基礎方程式、化学反応の速度式、情報理論におけるエントロピーの計算、経済学の複利モデルなど、どの分野を見ても「e」と自然対数は静かに姿を現す。表面上は見えにくいが、それは空気のように、世界の根本構造を支える存在といってよいだろう。
本記事では、この「自然対数」という奥深い概念を、数学的な定義だけでなく、その歴史的背景、応用の実例、社会的意義、そして私たちの思考に与える影響までを含めて丁寧に解きほぐしていく。単なる数の知識ではなく、「なぜこの数が自然界と人間社会の根底にあるのか」「なぜそれが“自然”と呼ばれるのか」という問いを出発点に、自然対数という名の扉を一緒に開いていこう。
自然対数の本質を理解するために、まずは「指数」と「対数」という基本的な考え方から出発しよう。難しそうな言葉に見えても、それらは本来、「ものごとがどう変化していくのか」をとらえるためのシンプルな道具にすぎない。そして、その根底にあるのが「e(約2.71828)」という数であり、これは単なる数学的な定数ではなく、自然界の“変化のかたち”そのものを表す数である。


コメント